Ternary Search is a divide-and-conquer searching algorithm designed for sorted arrays. It works by dividing the search range into three equal parts and recursively narrowing down the range where the target element might be located. It is particularly useful for unimodal functions or when the search space is ordered and well-structured.
How Ternary Search Works?
Divide the Range:
Identify two midpoints in the array:
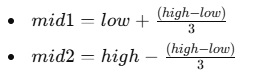
Compare with the Key:
- If the key matches the element at
mid1, returnmid1. - If the key matches the element at
mid2, returnmid2. - If the key is smaller than the element at
mid1, search the left segment [low, mid1−1]. - If the key lies between
mid1andmid2, search the middle segment [mid1+1, mid2−1]. - If the key is larger than the element at
mid2, search the right segment [mid2+1, high].
Recursive Search:
Repeat the process until the range becomes invalid or the key is found.
Ternary Search Program Examples
In this article, we’ll explore Ternary Search with two Java programs: a basic example for numeric arrays and an advanced implementation for searching within custom object lists.
1. Ternary Search Basic Program Example
This basic program uses Ternary Search on a sorted array to locate the target element by recursively dividing the range into three segments.
package com.javacodepoint.search;
public class BasicTernarySearch {
public static int ternarySearch(int[] array, int low, int high, int key) {
if (low <= high) {
int mid1 = low + (high - low) / 3;
int mid2 = high - (high - low) / 3;
if (array[mid1] == key) {
return mid1;
}
if (array[mid2] == key) {
return mid2;
}
if (key < array[mid1]) {
return ternarySearch(array, low, mid1 - 1, key);
} else if (key > array[mid2]) {
return ternarySearch(array, mid2 + 1, high, key);
} else {
return ternarySearch(array, mid1 + 1, mid2 - 1, key);
}
}
return -1;
}
public static void main(String[] args) {
int[] numbers = { 10, 20, 30, 40, 50, 60, 70, 80, 90 };
int key = 50;
int result = ternarySearch(numbers, 0, numbers.length - 1, key);
if (result != -1) {
System.out.println("Element found at index: " + result);
} else {
System.out.println("Element not found.");
}
}
}
OUTPUT:
Element found at index: 4
2. Ternary Search Advanced Program Example
This advanced program applies Ternary Search to a list of Product objects, finding a product based on its id. It highlights the algorithm’s flexibility in searching within complex data structures.
package com.javacodepoint.search;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
class Product {
private int id;
private String name;
public Product(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
@Override
public String toString() {
return "Product{id=" + id + ", name='" + name + "'}";
}
}
public class AdvancedTernarySearch {
public static int ternarySearch(List<Product> products, int low, int high, int key) {
if (low <= high) {
int mid1 = low + (high - low) / 3;
int mid2 = high - (high - low) / 3;
if (products.get(mid1).getId() == key) {
return mid1;
}
if (products.get(mid2).getId() == key) {
return mid2;
}
if (key < products.get(mid1).getId()) {
return ternarySearch(products, low, mid1 - 1, key);
} else if (key > products.get(mid2).getId()) {
return ternarySearch(products, mid2 + 1, high, key);
} else {
return ternarySearch(products, mid1 + 1, mid2 - 1, key);
}
}
return -1;
}
public static void main(String[] args) {
List<Product> products = new ArrayList<>();
products.add(new Product(101, "Laptop"));
products.add(new Product(102, "Tablet"));
products.add(new Product(103, "Smartphone"));
products.add(new Product(104, "Smartwatch"));
int key = 103;
// Sort products by ID
products.sort(Comparator.comparingInt(Product::getId));
int result = ternarySearch(products, 0, products.size() - 1, key);
if (result != -1) {
System.out.println("Product found: " + products.get(result));
} else {
System.out.println("Product not found.");
}
}
}
OUTPUT:
Product found: Product{id=103, name=’Smartphone’}
Ternary Search Efficiency

You can explore other search algorithms like Linear Search, Binary Search, Interpolation Search, Fibonacci Search, Exponential Search, and Jump Search.
