In this post, you will see how to Subtract the two Matrices in Java. Here, we will show you two examples, one with two static matrices, and another one with dynamic matrices.
Rules for the Subtraction of the two Matrices:
- The matrix subtraction can be done when the dimensions of matrices are the same.
- Matrix subtraction is the operation of subtracting two matrices by subtracting the corresponding entries.
- The resultant matrix dimension will be the same as matrix1 and matrix2.
Matrix Subtraction Example:
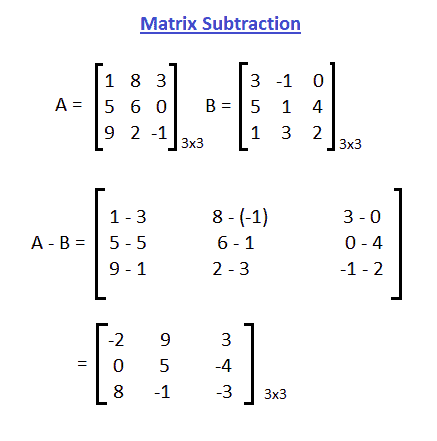
Example-1: Subtract two Matrices in Java
package com.javacodepoint.array.multidimensional;
/**
* Matrix Subtraction Example
*/
public class SubtractTwoMatrix {
public static void main(String[] args) {
// Declare and Initialize
// two Matrices of dimension 3x2
int matrix1[][] = { { 1, 2 },
{ 3, 4 },
{ 5, 6 }
};
int matrix2[][] = { { -1, 2 },
{ 2, -4 },
{ 1, 9 }
};
// Declare third matrix of same dimension 3x2
// to store the subtraction of two matrices
int matrix3[][] = new int[3][2];
// Subtract two matrices
for (int i = 0; i < matrix1.length; i++) {
for (int j = 0; j < matrix1[0].length; j++) {
matrix3[i][j] = matrix1[i][j] - matrix2[i][j];
}
}
// Print the result matrix
System.out.println("The resultant Matrix3 =>");
for (int i = 0; i < matrix3.length; i++) {
for (int j = 0; j < matrix3[0].length; j++) {
System.out.print(matrix3[i][j] + " ");
}
// move cursor to new row/line
System.out.println();
}
}
}
OUTPUT:
The resultant Matrix3 =>
2 0
1 8
4 -3
Example-2: Subtraction of two Matrices using Scanner in Java
package com.javacodepoint.array.multidimensional;
import java.util.Scanner;
/**
* Matrix Subtraction Example using Scanner
*/
public class SubtractTwoMatrix2 {
public static void main(String[] args) {
// Declare variables for matrix dimension
int row1, col1, row2, col2;
// Creating scanner object for reading user input
Scanner sc = new Scanner(System.in);
System.out.println("Enter the first matrix dimension,");
System.out.print("Row= ");
row1 = sc.nextInt();
System.out.print("Column= ");
col1 = sc.nextInt();
System.out.println("Enter the second matrix dimension,");
System.out.print("Row= ");
row2 = sc.nextInt();
System.out.print("Column= ");
col2 = sc.nextInt();
if (row1 != row2 || col1 != col2) {
System.out.println("Subtraction of Matrices is not possible. Dimensions of both matrices should match!");
return;
}
// Declare three Matrices
int matrix1[][] = new int[row1][col1];
int matrix2[][] = new int[row2][col2];
int matrix3[][] = new int[row1][col1]; // can be take row2/col2 as well
// Read the user inputs for matrix1
System.out.println("Enter Matrix1 (" + row1 + "x" + col1 + "),");
for (int i = 0; i < row1; i++) {
for (int j = 0; j < col1; j++) {
System.out.print("Enter value for [" + i + "][" + j + "]= ");
matrix1[i][j] = sc.nextInt();
}
}
// Read the user inputs for matrix2
System.out.println("Enter Matrix2 (" + row1 + "x" + col1 + "),");
for (int i = 0; i < row2; i++) {
for (int j = 0; j < col2; j++) {
System.out.print("Enter value for [" + i + "][" + j + "]= ");
matrix2[i][j] = sc.nextInt();
}
}
// Subtract two matrices
for (int i = 0; i < row1; i++) {
for (int j = 0; j < col1; j++) {
matrix3[i][j] = matrix1[i][j] - matrix2[i][j];
}
}
// Print the result matrix
System.out.println("The resultant Matrix3 (" + row1 + "x" + col1 + "),");
for (int i = 0; i < row1; i++) {
for (int j = 0; j < col1; j++) {
System.out.print(matrix3[i][j] + " ");
}
// move cursor to new row/line
System.out.println();
}
}
}
OUTPUT:
Enter the first matrix dimension,
Row= 3
Column= 3
Enter the second matrix dimension,
Row= 3
Column= 3
Enter Matrix1 (3×3),
Enter value for [0][0]= 1
Enter value for [0][1]= 2
Enter value for [0][2]= 3
Enter value for [1][0]= 4
Enter value for [1][1]= 5
Enter value for [1][2]= 6
Enter value for [2][0]= 7
Enter value for [2][1]= 8
Enter value for [2][2]= 9
Enter Matrix2 (3×3),
Enter value for [0][0]= 1
Enter value for [0][1]= 2
Enter value for [0][2]= 3
Enter value for [1][0]= 1
Enter value for [1][1]= 2
Enter value for [1][2]= 3
Enter value for [2][0]= 1
Enter value for [2][1]= 2
Enter value for [2][2]= 3
The resultant Matrix3 (3×3),
0 0 0
3 3 3
6 6 6
See also:
Java Program to Add the Two Matrices.
Java Program to Find the Sum of an Array.
Java Program to Count the Number of Vowels in a String.
