Interpolation Search is an optimized searching algorithm for sorted datasets that works by estimating the position of the target element based on the values at the boundaries. It assumes that the dataset is uniformly distributed and calculates the probable position of the key using the formula:
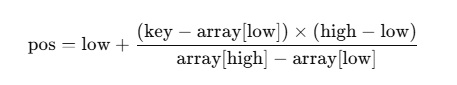
Unlike Binary Search, which always checks the middle, Interpolation Search adjusts the position dynamically based on the key’s proximity to boundary values. It performs best with large, uniformly distributed data, achieving an average time complexity of O(log logn).
How Interpolation Search Works?
Here’s how it works step by step:
1. Initialization:
Start with two-pointers, low and high, representing the start and end of the dataset.
2. Estimate the Position:
Calculate the position of the key using the formula:
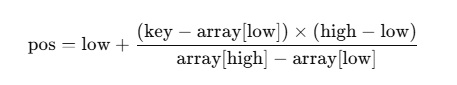
This formula predicts the position of the key by proportionally dividing the range between low and high based on the key’s value.
3. Comparison:
- If the key matches the value at
array[pos], the search is successful, and the index is returned. - If the key is smaller than
array[pos], adjust thehighpointer topos - 1and search the left subarray. - If the key is larger than
array[pos], adjust thelowpointer topos + 1and search the right subarray.
4. Repeat: Continue recalculating pos and narrowing down the search range until:
- The key is found.
- The search range becomes invalid (
low > high) or the key is outside the range.
5. Return Result: If the key is found, return its index; otherwise, return -1.
Interpolation Search Java Program Examples
In this article, we’ll explore Interpolation Search through two Java programs: a basic example for numeric arrays and an advanced implementation for searching within custom object lists.
1. Interpolation Search Basic example
This program example demonstrates an Interpolation Search for a sorted array of integers.
package com.javacodepoint.search;
public class BasicInterpolationSearch {
public static int interpolationSearch(int[] array, int key) {
int low = 0;
int high = array.length - 1;
while (low <= high && key >= array[low] && key <= array[high]) {
if (low == high) {
if (array[low] == key)
return low;
return -1;
}
// Estimate position
int pos = low + ((key - array[low]) * (high - low)) / (array[high] - array[low]);
// Check if the key is found
if (array[pos] == key) {
return pos;
}
// If the key is larger, search the right side
if (array[pos] < key) {
low = pos + 1;
} else { // If the key is smaller, search the left side
high = pos - 1;
}
}
return -1; // Key not found
}
public static void main(String[] args) {
int[] numbers = { 10, 20, 30, 40, 50, 60, 70, 80, 90 };
int key = 70;
int result = interpolationSearch(numbers, key);
if (result != -1) {
System.out.println("Element found at index: " + result);
} else {
System.out.println("Element not found.");
}
}
}
OUTPUT:
Element found at index: 6
2. Interpolation Search Advanced Program Example
This advanced program example applies the algorithm to a list of custom Product objects, enabling a search based on the price property.
package com.javacodepoint.search;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
class Product {
private int price;
private String name;
public Product(int price, String name) {
this.price = price;
this.name = name;
}
public int getPrice() {
return price;
}
@Override
public String toString() {
return "Product{name='" + name + "', price=" + price + "}";
}
}
public class AdvancedInterpolationSearch {
public static int interpolationSearch(List<Product> products, int key) {
int low = 0;
int high = products.size() - 1;
while (low <= high && key >= products.get(low).getPrice() && key <= products.get(high).getPrice()) {
if (low == high) {
if (products.get(low).getPrice() == key)
return low;
return -1;
}
// Estimate position
int pos = low + ((key - products.get(low).getPrice()) * (high - low))
/ (products.get(high).getPrice() - products.get(low).getPrice());
// Check if the key is found
if (products.get(pos).getPrice() == key) {
return pos;
}
// If the key is larger, search the right side
if (products.get(pos).getPrice() < key) {
low = pos + 1;
} else { // If the key is smaller, search the left side
high = pos - 1;
}
}
return -1; // Key not found
}
public static void main(String[] args) {
List<Product> products = new ArrayList<>();
products.add(new Product(100, "Laptop"));
products.add(new Product(200, "Smartphone"));
products.add(new Product(300, "Tablet"));
products.add(new Product(400, "Smartwatch"));
int key = 300;
// Sort products by price
products.sort(Comparator.comparingInt(Product::getPrice));
int result = interpolationSearch(products, key);
if (result != -1) {
System.out.println("Product found: " + products.get(result));
} else {
System.out.println("Product not found.");
}
}
}
OUTPUT:
Product found: Product{name=’Tablet’, price=300}
Key Points
- Requirements: The dataset must be sorted and preferably uniformly distributed.
- Efficiency:
- Best case: O(log logn).
- Worst case: O(n), when the data is highly skewed.
You can explore other search algorithms like Linear Search, Binary Search, Fibonacci Search, Exponential Search, Ternary Search, and Jump Search.
